M_Map: User's Guide v1.3d

1. Getting started

First, get all the files, either as a zip archive or a gzipped tar-file and unpack them. Now, start up Matlab (version 5 or higher). Make sure that the toolbox is in your path. This can be done simply by cd'ing to the correct directory.

Alternatively, if you have unpacked them into directory /users/rich/m_map (and /users/rich/m_map/private), then you can add this to your search path:

path(path,'/users/rich/m_map');

addpath /users/rich/m_map

(Note: you may want to install M_Map as a toolbox accessible to all users. To do this, unpack the files into $MATLAB/toolbox/m_map, and add that directory to the list defined in $MATLAB/toolbox/local/pathdef.m).

Instructions for installing the (optional) high-resolution bathymetry database are given in Section 9 , and instructions for installing the (optional) high-resolution GSHHS coastline database is given in Section 10 . However, we should first check that the basic setup is OK.

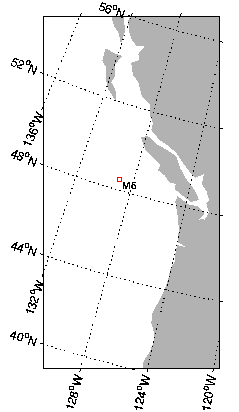
To see an example map, try this:

m_proj('oblique mercator');
m_coast;
m_grid;

The first line initializes the projection. Defaults are set for the different projection, so you can easily see what a specific projection looks like, but all projections have a number of optional parameters as well. To get the same map without using the defaults, you would use

m_proj('oblique mercator','longitudes',[-132 -125], ...
       'latitudes',[56 40],'direction','vertical','aspect',.5);

The second line draws a coastline, using the 1/4 degree database. Coastlines with greater resolution can be drawn, using your own database (see also Section 7 ). m_coast can be called with various line parameters. For example,

m_coast('linewidth',2,'color','r');

m_coast('patch',[.7 .7 .7],'edgecolor','none');

The third line superimposes a grid. Although there are many possible options that can be used to customize the appearance of the grid, defaults can always be used (as in the example). These options are discussed in Section 4 . You can get a list of the options using the GET syntax:

m_grid get

Finally, suppose you want to show and label the location of, say, a mooring at 129W, 48 30'N.

[X,Y]=m_ll2xy(-129,48.5);
line(X,Y,'marker','square','markersize',4,'color','r');
text(X,Y,' M5','vertical','top');

m_ll2xy (and its inverse m_xy2ll) convert from longitude/latitude coordinates to those of the projection. Various clipping options can also be specified in converting to projection coordinates. If you are willing to accept default clipping setting, you can use the built-in functions m_line and m_text :

m_line(-129,48.5,'marker','square','markersize',4,'color','r');
m_text(-129,48.5,' M5','vertical','top');

Finally (!), we may want to alter the grid details slightly. Note that, a given map must only be initialized once.

clf
m_coast('patch',[.7 .7 .7],'edgecolor','none');
m_grid('xlabeldir','end','fontsize',10);
m_line(-129,48.5,'marker','square','markersize',4,'color','r');
m_text(-129,48.5,' M5','vertical','top');

2. Specifying projections

In order to get a list of the current projections,

m_proj get

m_proj('get');

Available projections are:
     Stereographic
     Orthographic 
     Azimuthal Equal-area
     Azimuthal Equidistant
     Gnomonic
     Satellite
     Albers Equal-Area Conic
     Lambert Conformal Conic
     Mercator
     Miller Cylindrical
     Equidistant Cylindrical
     Oblique Mercator
     Transverse Mercator
     Sinusoidal
     Gall-Peters
     Hammer-Aitoff
     Mollweide
     UTM

m_proj('get','stereographic');
     'Stereographic'                                   
     <,'lon<gitude>',center_long>                      
     <,'lat<itude>', center_lat>                       
     <,'rad<ius>', ( degrees | [longitude latitude] )>
     <,'rec<tbox>', ( 'on' | 'off' )>                  

m_proj('sinusoidal');
m_proj set
Current mapping parameters -
 Projection: Sinusoidal  (function: mp_tmerc)
 longitudes: -90  30 (centered at -30)       
 latitudes: -65  65                          
 Rectangular border: off                     

Two useful properties for projections are (1) the ability the preserve angles for differentially small regions, and (2) the ability to preserve area. Projections satisfying the first condition are called conformal , those satisfying the second are called equal-area . No projection can be both. Many projections (especially global projections) are neither, instead an attempt has been made to aesthetically balance the errors in both conditions.

Note: All projections (except UTM) are currently spherical rather than ellipsoidal. It is unlikely that this will be a problem in normal usage.

Azimuthal projections

Azimuthal projections are those in which points on the globe are projected onto a flat tangent plane. Maps using these projections have the property that direction or azimuth from the center point to all other points is shown correctly. Great circle routes passing through the central point appear as straight lines (although great circles not passing through the central point may appear curved). These maps are usually drawn with circular boundaries. The following parameters are needed to define an azimuthal projection:

<,'lon<gitude>',center_long>
<,'lat<itude>', center_lat>

These parameters define the center point of the map. Maps are aligned so that the specified longitude is vertical at the map center, with its northern end at the top.

<,'rad<ius>', ( degrees | [longitude latitude] )>

This defines the extent of the map. Either an angular distance in degrees can be given (e.g. 90 for a hemisphere), or the coordinates of a point on the boundary can be specified.

<,'rec<tbox>', ( 'on' | 'off' | 'circle' )>

The default is to enclose the map in a circular boundary (chosen using either of the latter two options), but a rectangular one can also be specified. However, rectangular maps are usually better drawn using a cylindrical or conic projection of some sort.

Stereographic

The stereographic projection is conformal, but not equal-area. This projection is often used for polar regions.

Orthographic

This projection is neither equal-area nor conformal, but resembles a perspective view of the globe.

Azimuthal Equal-Area

Sometimes called the Lambert azimuthal equal-area projection, this mapping is equal-area but not conformal.

Azimuthal Equidistant

This projection is neither equal-area nor conformal, but all distances and directions from the central point are true.

Gnomonic

This projection is neither equal-area nor conformal, but all straight lines on the map (not just those through the center) are great circle routes. There is, however, a great degree of distortion at the edges of the map, so maximum radii should be kept fairly small - 20 or 30 degrees at most.

Satellite

This is a perspective view of the earth, as seen by a satellite at a specified altitude. Instead of specifying a radius for the map, the viewpoint altitude is specified:

<,'alt<itude>', altitude_fraction >

the numerical value assigned to this property represents the height of the viewpoint in units of earth radii. For example, a satellite in an orbit of radius 3 earth radii would have an altitude of 2.

Cylindrical and Pseudo-cylindrical Projections

Cylindrical projections are formed by projecting points onto a plane wrapped around the globe, touching only along some great circle. These are very useful projections for showing regions of great lateral extent, and are also commonly used for global maps of mid-latitude regions only. Also included here are two pseudo-cylindrical projections, the sinusoidal and Gall-Peters, which have some similarities to the cylindrical projections (see below).

These maps are usually drawn with rectangular boundaries (with the exception of the sinusoidal and sometimes the transverse mercator).

Mercator

This is a conformal map, based on a tangent cylinder wrapped around the equator. Straight lines on this projection are rhumb lines (i.e. the track followed by a course of constant bearing). The following properties affect this projection:

<,'lon<gitude>',( [min max] | center)>

Either longitude limits can be set, or a central longitude defined implying a global map.

<,'lat<itude>', ( maxlat | [min max])>

Latitude limits are most usually the same in both N and S latitude, and can be specified with a single value, but (if desired) unequal limits can also be used.

Miller Cylindrical

This projection is neither equal-area nor conformal, but "looks nice" for world maps. Properties are the same as for the Mercator, above.

Equidistant cylindrical

This projection is neither equal-area nor conformal. It consists of equally-spaced latitude and longitude lines, and is very often used for quick plotting of data. It is included here simply so that such maps can take advantage of the grid generation routines. Also known as the Plate Carree. Properties are the same as for the Mercator, above.

Oblique Mercator

The oblique mercator arises when the great circle of tangency is arbitrary. This is a useful projection for, e.g., long coastlines or other awkwardly shaped or aligned regions. It is conformal but not equal area. The following properties govern this projection:

<,'lon<gitude>',[ G1 G2 ]>
<,'lat<itude>', [ L1 L2 ]>

Two points specify a great circle, and thus the limits of this map (it is assumed that the region near the shortest of the two arcs is desired). The 2 points (G1,L1) and (G2,L2) are thus at the center of either the top/bottom or left/right sides of the map (depending on the 'direction' property).

<,'asp<ect>',value>

This specifies the size of the map in the direction perpendicular to the great circle of tangency, as a proportion of the length shown. An aspect ratio of 1 results in a square map, smaller numbers result in skinnier maps. Aspect ratios >1 are possible, but not recommended.

<,'dir<ection>',( 'horizontal' | 'vertical' )

This specifies whether the great circle of tangency will be horizontal on the page (for making short wide maps), or vertical (for tall thin maps).

Transverse Mercator

The Transverse Mercator is a special case of the oblique mercator when the great circle of tangency lies along a meridian of longitude, and is therefore conformal. It is often used for large-scale maps and charts. The following properties govern this projection:

<,'lon<gitude>',[min max]>
<,'lat<itude>',[min max]>

These specify the limits of the map.

<,'clo<ngitude>',value>

Although it makes most sense in general to specify the central meridian as the meridian of tangency (this is the default), certain map classification systems (noteably UTM) use only a fixed set of central longitudes, which may not be in the map center.

<,'rec<tbox>', ( 'on' | 'off' )>

The map limits can either be based on latitude/longitude (the default), or the map boundaries can form an exact rectangle. The difference is small for large-scale maps. Note: Although this projection is similar to the Universal Transverse Mercator (UTM) projection, the latter is actually ellipsoidal in nature.

Universal Transverse Mercator (UTM)

UTM maps are needed only for high-quality maps of small regions of the globe (less than a few degrees in longitude). This is an ellipsoidal projection. Options are similar to those of the Transverse Mercator, with the addition of

<,'zon<e>', value 1-60>

<,'hem<isphere>',value 0=N,1=S>

These are computed automatically if not specified. The ellipsoid defaults to 'normal', a spherical earth of radius 1 unit, but other options can also be chosen using the following property:

<,'ell<ipsoid>', ellipsoid>

For a list of available ellipsoids try m_proj('get','utm').

The big difference between UTM and all the other projections is that for ellipsoids other than 'normal' the projection coordinates are in meters of easting and northing. To take full advantage of this it is often useful to call m_proj with 'rectbox' set to 'on' and not to use the long/lat grid generated by m_grid (since the regular matlab grid will be in units of meters).

Sinusoidal

This projection is usually called "pseudo-cylindrical" since parallels of latitude appear as straight lines, similar to their appearance in cylindrical projections tangent to the equator. However, meridians curve together in this projection in a sinusoidal way (hence the name), making this map equal-area.

Gall-Peters

Parallels of latitude and meridians both appear as straight lines, but the vertical scale is distorted so that area is preserved. This is useful for tropical areas, but the distortion in polar areas is extreme.

Conic Projections

Conic projections result from projecting onto a cone wrapped around the sphere. The vertex of the cone lies on the rotational axis of the sphere. The cone is either tangent at a single latitude, or can intersect the sphere at two separated latitudes. It is a useful projection for mid-latitude areas of large east-west extent. The following properties affect these projections:

<,'lon<gitude>',[min max]>
<,'lat<itude>',[min max]>

These specify the limits of the map.

<,'clo<ngitude>',value>

The central longitude appears as a vertical on the page. The default value is the mean longitude, although it may be set to any value (even one outside the limits).

<,'par<allels>',[lat1 lat2]>

The standard parallels can be specified. Either one or two parallels can be given, the default is a single parallel at the mean latitude

<,'rec<tbox>', ( 'on' | 'off' )>

The map limits can either be based on latitude/longitude (the default), or the map boundaries can form an exact rectangle which contain the given limits. Unless the region being mapped is small, it is best to leave this 'off' .

Albers Equal-Area Conic

This projection is equal-area, but not conformal

Lambert Conformal Conic

This projection is conformal, but not equal-area.

Miscellaneous global projections

There are a number of projections which don't really fit into any of the above categories. Mostly these are global projections (i.e. they show the whole world), and they have been designed to be "pleasing to the eye". I'm not sure what use they are in general, but they make nice logos!

Hammer-Aitoff

An equal-area projection with curved meridians and parallels.

Mollweide

Also called the Elliptical or Homolographic Equal-Area Projection. Parallels are straight (and parallel) in this projection. Note that example 4 shows a rather sophisticated use designed to reduce distortion, a more standard map can be made using

m_proj('mollweide');
m_coast('patch','r');
m_grid('xaxislocation','middle');

Yeah, but which projection should I use?

Well, it depends really on how large an area you are mapping. Usually, maps of the whole world are Mercator, although often the Miller Cylindrical projection looks better because it doesn't emphasize the polar areas as much. Another choice is the Hammer-Aitoff or Mollweide (which has meridians curving together near the poles). Both are equal-area. It's probably not a good idea to use these projections for maps that don't have the equator somewhere near the middle.

If you are plotting something with a large north/south extent, but not very wide (say, North and South America, or the North and South Atlantic), then the Sinusoidal or Mollweide projections will look pretty good. Another choice is the Transverse Mercator, although that is usually used only for very large-scale maps.

For smaller areas within one hemisphere or other (say, Australia, the United States, the Mediterranean, the North Atlantic) you might pick a conic projection. The differences between the two available conic projections are subtle, and if you don't know much about projections it probably won't make much difference which one you use.

If you get smaller than that, it doesn't matter a whole lot which projection you use. One projection I find useful in many cases is the Oblique Mercator, since you can align it along a long (but narrow) coastal area. If map limits along lines of longitude/latitude are OK, use a Transverse Mercator or Conic Projection. The UTM projection is also useful.

Polar areas are traditionally mapped using a Stereographic projection, since for some reason it looks nice to have a "bullseye" pattern of latitude lines.

If you want to get a quick idea of what any projection looks like, default parameters for all functions are set for a "typical" usage, i.e. to get a quick idea of what any projection looks like, you can do so without having to figure out a lot of numerical values:

m_proj('stereographic');  % Example for stereographic projection
m_coast;
m_grid;

Map scales

M_Map usually scales the map so that it fits exactly within the current axes. If you just want a nice picture (which is mostly the case) then this is exactly what you need. On the other hand, sometimes you want to print things out at some exact scale (i.e. if you really much prefer sitting at your desk with a ruler and a piece of paper trying to figure out how far apart Bangkok and Tokyo are). Use the m_scale primitive for this - for a 1:250000 map, call

m_scale(250000);

after you have drawn everything (Be careful - a 1:250000 map of the world is a lot bigger than 8.5"x11" sheet of paper).

This option is usually only useful for large-scale maps, i.e. maps of very small areas).

If you wish to know the current scale, calling m_scale without any parameters will calculate and return that value.

To return to the default scaling call m_scale('auto').

(PS - If you do want to find distances from Bangkok to anywhere, plot an azimuthal equidistant projection of the world centered on Bangkok (13 44'N, 100 30'E), and choose a fairly small scale, like 1:200,000,000). Another option would be to use range rings, see example 11.

3. Coastlines and Bathymetry

M_Map includes two fairly simple databases for coastlines and global elevation data. Highly-detailed databases are not included in this release because they are a) extremely large and b) extremely time-consuming to process (loops are inherently involved). If more detailed maps are required, section 9 and section 10 give instructions on how to add some freely-available high-resolution datasets. Read section 7 and section 8 if you want to add your own coastline/bathymetry data.

Coastline options

M_Map includes a 1/4 degree resolution coastline database. This is suitable for maps covering large portions of the globe, but is noticeably coarse for many large-scale applications. Users not satisfied with their regional map are directed to section 7 and/or section 10 for more information on creating and using high-resolution coastlines. The M_Map database is accessed using the m_coast function. Coastlines can be drawn as simple lines, using

m_coast('line', ...optional line arguments );

or

m_coast( optional line arguments );

where the optional arguments are all the standard arguments for specifying line style, width, color, etc. Coastlines can also be drawn as filled patches using

m_coast('patch', ...optional patch arguments );

where the optional trailing arguments are the standard patch properties. For example,

m_coast('patch',[.7 .7 .7],'edgecolor','g');

draws gray land, outlined in green. When patches are being drawn, lakes and inland seas are given the axes background colour.

Note that line coastlines are usually drawn rather rapidly. Filled coastlines take considerably more time to generate (because map limits are not necessarily rectangular, clipping must be accomplished in m-files).

Topography/Bathymetry options

M_Map can access a 1-degree resolution global elevation database (actually, this database is is included in the Matlab distribution, used by of $MATLAB/toolbox/matlab/demos/earthmap.m). A contour map of elevations at default levels can be drawn using

m_elev;

Different levels can also be specified:

m_elev('contour',LEVELS, optional contour arguments);

For example, if you want all the contours to be dark blue, use:

m_elev('contour',LEVELS,'edgecolor','b');

Filled contours are also possible:

m_elev('contourf',LEVELS, optional contourf arguments);

Finally, if you want to simply extract the elevation data for your own purposes,

[Z,LONG,LAT]=m_elev([LONG_MIN LONG_MAX LAT_MIN LAT_MAX]);

returns rectangular matrices for depths Z at locations LONG,LAT.

4. Customizing axes

Grid lines and labels

In order to get the perfect grid, you may want to experiment with different grid options. Two functions are useful here, M_GRID which draws a grid, and M_UNGRID which erases the current grid (but leaves all coastlines and user-specified data alone). Try

m_proj('Lambert');
m_coast;
m_grid;

to get a Lambert conic projection of North America. Now try

m_ungrid

The coastline is still there, but the grid has disappeared and the axes shows raw X/Y projection coordinates. Now, try this:

m_grid('xtick',10,'tickdir','out','yaxislocation','right','fontsize',7);

The various options that can be changed are:

'box',( 'on' | 'off' | 'fancy' )

This specifies whether or not an outline box is drawn. Three types of outline boxes are available: 'on', the default, is a a simple line. Two types of fancy outline boxes are available. If 'tickdir' is 'in', then alternating black and white patches are made (see example 2). If 'tickdir' is set to 'out', then a more complex line pattern is drawn (see example 6). Fancy boxes are in general only available for maps bounded by lat/long limits (i.e. not for azimuthal projections), but if this option is chosen inappropriately a warning message is issued.

'xtick',( num | [value1 value2 ...])

This specifies the number/location of the longitude grid. If a single number is specified, grid lines/values are drawn for approximately that number of equally-spaced locations (the number is only approximate because the M_GRID attempts to find "nice" intervals, i.e. it rounds to even increments). Exact locations can be specified by using a vector of location values. There is an analagous 'ytick' property.

'xticklabels',[label1;label2 ...]

Special labels can be specified. Labels can either be numerical values (which are then formatted by M_GRID), or string values which are used without change. There is an analagous 'yticklabels' property

'xlabeldir', ( 'middle' | 'end' )

Longitude labels are either middled onto the ends of their prespective grid lines (and drawn perpendicular to those lines), or are drawn extending outwards fro the ends of those lines. There is an analagous 'ylabeldir' property.

'ticklen',value

Specifies the length of tickmarks (as a fraction of plot width)

'tickdir',( 'in' | 'out' )

Specifies whether tickmarks point inwards or outwards. If 'box' is set to 'fancy', this specifies the form of the fancy outline box.

'color',colorspec
'linewidth', value
'linestyle', ( linespec | 'none' )
'fontsize',value
'fontname',name

Specify various line/text properties for the grid and its labels.

'XaxisLocation',( 'bottom' | 'middle' | 'top' )

Specifies where the X-axis will be drawn, either at the bottom (southermost) end, at the top (northernmost) end, or in the middle.

'YaxisLocation',( 'left' | 'middle' | 'right' )

Specifies where the Y-axis will be drawn, either at the left (westernmostmost) end, at the right (easternmost) end, or in the middle.

Titles and x/ylabels

Titles and x/ylabels can be added to maps using the title and x/ylabel functions in the usual way (this is a change from v1.0 in which the 'visible' property had to be explicitly set to 'on'; this is now done within m_grid).

5. Adding your own data

The purpose of this package is to allow you to map your own data! Once a suitable grid and (possibly) a coastline have been chosen, you can add your own lines, text, or contour plots using built-in M_Map drawing functions which handle the conversion from longitude/latitude coordinates to projection coordinates. These drawing functions are very similar to the standard Matlab plotting functions, and are described in the next section.

Sometimes you may want to convert between longitude/latitude and projection coordinates without immediately plotting the data. This might happen if you want to interactively select points using ginput, or if you want to draw labels tied to a specific point on the screen rather than a particular longitude/latitude. Projection conversion routines are described in sections 5.2 and 5.3. Once raw longitude/latitude coordinates are converted into projection coordinates, standard Matlab plotting functions can be used.

Maps are drawn to fit within the boundaries of the plot axes. Thus their scale is somewhat arbitrary. If you are interested in making a map to a given scale, e.g. 1:200000 or something like that, you can do so by using the m_scale primitive, see section 2.6 . The data units are the projection coordinates, which are distances expressed as a fraction of earth radii. To get a map "distance" between two points, use the Cartesian distance between the points in the projection coordinate system and multiply by your favourite value for the earth's radius, usually around 6370 km (exception - the UTM projection uses coordinates of northing and easting in meters, so no conversion is necessary).

Caution: One problem that sometimes occurs is that data does not appear on the plot due to ambiguities in longitude values. For example, if plot longitude limits are [-180 180], a point with a longitude of, say, 200, may not appear in cylindrical and conic projections. This is not a bug. Handling the clipping in "wrapped around" curves requires adding points (rather than just moving them) and is therefore incompatible with various other requirements (such as keeping input and output matrices the same size in the conversion routines described below).

Drawing lines, text, arrows, patches and contours

For most purposes you do not need to know what the projection coordinates actually are - you just want to plot something at a specified longitude/latitude. Most of the time you when you want to plot something on a map you want to do so by specifying longitude/latitude coordinates, instead of the usual X/Y locations. To do so in M_Map, replace calls to line, text, quiver, patch, contour, and contourf with M_Map equivalents that recognize lontgitude/latitude coordinates by prepending "m_" to the function name. For example,

m_line(LONG,LAT,...line properties)   % draw a line on a map
m_quiver(LONG,LAT,U,V,S)              % A quiver plot
m_text(LONG,LAT,'string')             % Text
m_patch(LONG,LAT,..patch properties)  % Patches.

Each of these functions will handle the coordinate conversion internally, and will return a vector of handles to the graphic objects if desired. The only difference between these functions and the standard Matlab functions is that the first two arguments MUST be longitude and latitude.

One caveat applies to m_patch. For compatibility reasons this uses the same code that applies to coastline filling. Coastlines come either as either "islands" or "lakes", and M_Map keeps track of the difference by assuming curves are oriented so that the filled area ("land") is always on the right as we go around the curve. This is slightly different than the convention used in patch which always fills the inside. Keeping track of this difference is relatively straightforward in a Cartesian system, but not so easy in spherical coordinates. In the absence of other information m_patch tries to do the right thing, but (especially when the patch intersects a map boundary) it can get confused. If a patch isn't filling correctly, try reversing the order of points using flipud or fliplr.

Data gridded in longitude and latitude can also be contoured:

m_contour(LONG,LAT,VALUES)
m_contourf(LONG,LAT,VALUES)

Again, these functions will return handles to graphics objects, allowing (for example) the drawing of labelled contours:

[cs,h]=m_contour(LONG,LAT,VALUES)
clabel(cs,h,'fontsize',6);

Fancy arrows (i.e. with width, head shape, and colour specifications) can be generated using m_vec.m . See the on-line help for more details about the use of m_vec.

Drawing tracklines

It is sometimes useful to annotate lines representing the time-varying location of a ship, aircraft, or satellite with time and date annotations. This can be done using m_track.

m_proj('UTM','long',[-72 -68],'lat',[40 44]);
m_gshhs_i('color','k');
m_grid('box','fancy','tickdir','out');

% fake up a trackline
lons=[-71:.1:-67];
lats=60*cos((lons+115)*pi/180);
dates=datenum(1997,10,23,15,1:41,zeros(1,41));

m_track(lons,lats,dates,'ticks',0,'times',4,'dates',8,...
        'clip','off','color','r','orient','upright');  


See the on-line help for more details about the use of m_track, and the different options for setting fontsize, tick spacing, date formats, etc.

While fiddling with the various parameters, it is often handy to be able to erase the plotted tracks without erasing the coastline and grid. This can be done using

m_ungrid track

or

m_ungrid('track')

Drawing range rings

One nifty thing that is sometimes useful is the ability to draw circles at a given range or ranges from a specific location. This can be done using m_range_ring, which has 3 required calling parameters: LONG, LAT, RANGE, followed by any number of (optional) line specification property/value pairs. Example 11 illustrates how to use m_range_ring.

Converting longitude/latitude to projection coordinates

If you want to use projection coordinates (perhaps you want to compute map areas, or distances, or you want to make a legend in the upper left corner), the following command converts longitude/latitude coordinates to projection coordinates.

[X,Y]=m_ll2xy(LONG,LAT, ...optional clipping arguments )

where LONG, LAT, X, and Y are matrices of the same size. Projection coordinates are equal to true distances near the center of the map, and are expressed as fractions of an earth radius. To get a distance, multiply by the radius of the earth (about 6370km). The exception is the UTM projection which provides coordinates of northing and easting in meters.

The possible clipping arguments are

'clip','on'

This is the default. Columns of LONG and LAT are assumed to form lines, and these are clipped to the map limits. The first point outside the map is therefore moved to the map edge, and all other points are converted the NaN.

'clip','off'

No clipping is performed. This is sometimes useful for debugging purposes.

'clip','point'

Points are tested against the map limits. Those outside the limits are converted to NaN, those inside are converted to projection coordinates. No points are moved. This option is useful for point data (such as station locations).

'clip','patch'

Points are tested against the map limits. Those outside the limits changed into a point exactly on the limits. Those inside are converted to projection coordinates. This option may be useful when trying to draw patches, however it probably won't work well.

Converting projection coordinates to longitude/latitude

Conversion from projection coordinates to longitude/latitude is straightforward:

[LONG,LAT]=m_xy2ll(X,Y)

There are no options.

6. More complex plots

For ideas on how to make more complex plots, see the Examples. These plots are also included in the function m_demo.

7. Removing data from a plot

Once a given map includes several elements a certain amount of fiddling is usually necessary to satisfy the natural human urge to give the image a certain aesthetic quality. If the image includes complicated coastlines which take a long time to draw (e.g. those discussed below) than clearing the figure and redrawing soon becomes tedious. The m_ungrid command introduced above can be used to selectively remove parts of the figure. For example:

m_proj('lambert','long',[-160 -40],'lat',[30 80]);
m_coast;
m_range_ring(-123,49,[1e3:1e3:10e3],'color','r');

m_ungrid range_ring
m_range_ring(-123,49,[200:200:2000],'color','r');

m_ungrid can recognize and delete specific elements by searching the 'tag' property of all plot elements, which is set by the various different M_Map routines.

8. Adding your own coastlines

If you are interested in a particular area and want a higher-resolution coastline than that used by m_coast, the best procedure is to

1. Get a subset of points from some high-resolution database, and
2. convert to screen coordinates using m_ll2xy, and plot.

load coast.dat
m_line(coast(:,1),coast(:,2));

load coast.dat
[X,Y]=m_ll2xy(coast(:,1),coast(:,2),'clip','patch');
k=[find(isnan(X(:,1)))];
for i=1:length(k)-1,
    x=coast([k(i)+1:(k(i+1)-1) k(i)+1],1);
    y=coast([k(i)+1:(k(i+1)-1) k(i)+1],2);
    patch(x,y,'r');
end;

DCW political boundaries

Files containing political boundaries for various countries and US states can be downloaded from http://www.maproom.psu.edu/cgi-bin/ian/points/index.cgi. Once downloaded to your machine use m_plotbndry to access and plot the desired boundary. For example, if you downloaded various US states into a subdirectory "states:,

m_plotbndry('states/arizona','color,'r')

would plot arizona on the current map.

9. Adding your own topography/bathymetry

A number of global and regional topography databases are available at NCAR . Several are available for free from their ftp site.

As long as the data is stored in a mat-file as a rectangular matrix in longitude/latitude, then m_contour or m_contourf can be used to plot that data.

Sandwell and Smith Bathymetry

A recent new bathymetry with approximately 1km resolution in lower latitude areas is being used by many people. This dataset is described at http://topex.ucsd.edu/marine_topo/text/topo.html and is available as a 134Mb binary file at ftp://topex.ucsd.edu/pub/global_topo_2min/topo_6.2.img . The authors have included an m-file (mygrid_sand.m) which can extract portions of the data. Once this database (and the m-file) is installed on your computer, you can use it in M_Map very easily. A typical usage is as follows:

% Extract data
[elevations,lat,lon]=mygrid_sand([lat_south lat_north long_west long_east]);

% Use in M_Map command
m_contour(lon,lat,elevations);

For some projections, you must make sure that the 'lon' values returned by mygrid_sand.m fall within the range used in this projection (i.e. you may have to add/subtract 360). This seems to happen all the time for areas in the west (i.e. negative longitudes), if you forget this you often end up with bewildering error messages about empty vectors!

10. Using TerrainBase 5-minute global bathymetry/topography

For many purposes the elevation database accessed by M_Map provides adequate resolution. However, there are also many cases when more detail is desired. I have not included a higher-resolution database because it would greatly increase the size of the package. However, v1.2 includes m-files to access and plot a popular global 5-minute bathymetry/topography database, after a few minutes of work.

This section provides instructions on how to download TerrainBase, and convert it from a 56Mb ASCII file to a 18Mb binary file using m_tba2b.m. It is then straightforward to access and plot bathymetry from this file using m_tbase.m, which is in every way functionally identical to m_elev (see Section 3.2).

TerrainBase is also available on CDrom, and is also commonly stored in netcdf (or other) binary format somewhere on many academic networks. If you modify m_tbase.m to access data from one of these sources, let me know!

How to install TerrainBase:

1. get and uncompress the tbase.Z file from ftp://ncardata.ucar.edu/datasets/ds759.2/tbase.Z into the m_map directory.

2. Run m_tba2b('PATHNAME') to store the resulting 18Mb binary file as PATHNAME/tbase.int.

3. Delete the original ASCII file tbase.

4. Edit the PATHNAME setting in m_tbase to point to the location of this file.

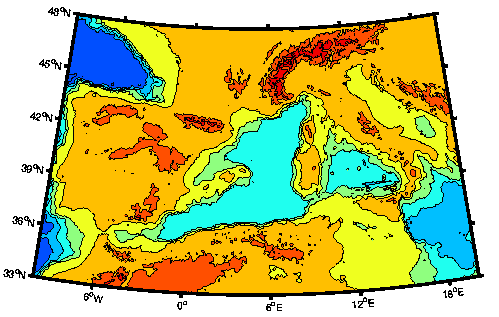
m_proj('lambert','lon',[-10 20],'lat',[33 48]);
m_tbase('contourf');
m_grid('linestyle','none','tickdir','out','linewidth',3);

11. Using GSHHS high-resolution coastline database

Installing GSHHS

When drawing maps there is always a tradeoff between the execution time of the generating program and the resolution of the resulting map. Included in M_Map is a 1/4 degree coastline database which can be used to generate very fast maps, with adequate resolution for many purposes.

However, it is often desirable to be able to make detailed maps of limited geographic areas. For this purpose a higher-resolution coastline database is necessary. I have not included such a database in M_Map because it would greatly increase the size of the package. However, I have included m-files to access and use a popular high-resolution database called GSHHS

As distributed, GSHHS consists of a hierarchical set of databases at different resolutions. The lowest or "crude" resolution is not as good as the M_Map database, although it contains many more inland lakes. The "high" resolution consists of points about 200m apart. There is also an even finer "full" resolution. You can install part or all of the database (depending on how much disk space you have available). The "full" resolution occupies 90Mb of disk space, and successively coarser resolutions are smaller by about 1/4. Thus "high" resolution occupies 21Mb, "intermediate" uses 6Mb, and "low" uses 1.1Mb (one reason for not always using "high" resolution is that the entire 90Mb database must be read and processed each call, which may take some time).

How to install GSHHS:

1. Go to ftp://ftp.ngdc.noaa.gov/MGG/shorelines/ .
2. Get and uncompress any or all of the files gshhs_c.b.gz, gshhs_l.b.gz, gshhs_i.b.gz and/or gshhs_h.b.gz in a convenient directory. One useful place is in m_map/private.
3. If the database files are not in subdirectory m_map/private , you must edit the FILNAME settings in m_gshhs_c.m, m_gshhs_l.m, m_gshhs_i.m, m_gshhs_h.m and/or m_gshhs_f.m to point to the appropriate files.

Using GSHHS effectively

The simplest calling mechanism is identical to that for m_coast ( Section 3 ). For example, to draw a gray-filled high-resolution coastline,

m_gshhs_h('patch',[.5 .5 .5]);

is sufficient. However, execution times may be very, very long, as the entire database must be searched and processed. I would not recommend trying to draw world maps with the intermediate or high-resolution coastlines! There are two ways to speed this up. The first is merely to use a lower-resolution database, with fewer points. The second is useful if you are going to be repeatedly drawing a map (because, for example, it's the base figure for your work). In this case I recommend that you save an intermediate processed (generally smaller) file as follows:

m_proj ...  % set up projection parameters

% This command does not draw anything - it merely processes the 
% high-resolution database using the current projection parameters 
% to generate a smaller coastline file called "gumby"

m_gshhs_h('save','gumby');

% Now we can draw a few maps of the same area much more quickly

figure(1);
m_usercoast('gumby','patch','r');
m_grid;

figure(2);
m_usercoast('gumby','linewidth',2,'color','b');
m_grid('tickdir','out','yaxisloc','left');

etc.

12. M_Map toolbox contents and description

1. Contents.m - toolbox contents
2. m_demo.m - demonstrates a few maps.

1. m_proj.m - initializes projections

2. m_grid.m - draws grids
3. m_scale.m - forces map to a given scale

4. m_ungrid.m - erases map elements (if you want to change parameters)

5. m_coast.m - draws a coastline
6. m_elev.m - draws elevation data
7. m_tbase.m - draws elevation data from high-resolution database
8. m_gshhs_c.m - draws coastline from GSHHS crude database
9. m_gshhs_l.m - draws coastline from GSHHS low-resolution database
10. m_gshhs_i.m - draws coastline from GSHHS intermediate-resolution database
11. m_gshhs_h.m - draws coastline from GSHHS high-resolution database
12. m_gshhs_f.m - draws coastline from GSHHS full resolution database
13. m_plotbndry.m - draws a political boundary from the DCW
14. m_usercoast.m - draws a coastline using a user-specified subset database.

15. m_line.m - draws line data in map coords
16. m_text.m - adds text data in map coords
17. m_patch.m - adds patch data in map coords
18. m_quiver - draws arrows for vector data
19. m_contour - draws contour lines for gridded data
20. m_contourf - draws filled contours
21. m_track - draws annotated tracklines
22. m_range_ring - draws range rings

23. m_ll2xy.m - converts from long/lat to map coordinates
24. m_xy2ll.m - converts from map coordinates to long/lat

25. m_tba2b.m - used in installing high-resolution elevation database.

26. m_vec.m - fancy arrows

1. private/mp_azim.m - azimuthal projections
2. private/mp_cyl.m - cylindrical projections (equatorial)
3. private/mp_conic.m - conic projections
4. private/mp_tmerc.m - transverse cylindrical projections
5. private/mp_utm.m - elliptical universal transverse cylindrical projections
6. private/mp_omerc.m - oblique cylindrical projection

7. private/mu_util.m - various utility routines
8. private/mu_coast.m - routines to handle coastlines.
9. private/clabel.m - patched version of clabel (matlab v5.1 version does not contain capabilities for different text properties).

10. private/m_coasts.mat - coastline data

1. map.html - documentation intro
2. private/mapug.html - users guide
3. various .gif - examples.

13. Known Problems and Bugs

1. Running M_Map with Matlab5.0 (Student versions?) can sometimes produce errors since 5.0 has various bugs and "features" that do not appear in later versions. One in particular has cropped up - the file m_coast.mat is sometimes not found when using m_coast.m. The easiest solution is to put ../m_map/private into your path as well as ../m_map (in later versions matlab can find the mat-file).

2. Running M_Map on a PC with Matlab5.1 can sometimes produce a lot of

   > Warning: Divide by zero.
   

   messages. This is due to a bug in Matlab (actually due to the compiler TMW used) that results in an incorrect warning flag being set when dividing some numbers by NaN. You can safely ignore these errors and wait for v5.2

3. If plotted data is coloured white, this will be changed to black in the postscript output. This is due to the workings of the print command. In order to avoid this, set the figure background to white, i.e.

   set(gcf,'color','white')
   

4. If you are using filled contours, and the plot becomes "complicated" above a certain level, it sometimes appears as if the contours are not filling properly, i.e. you get a white map with contour lines but no colour.

   However, if you print the figure, the resulting postscript file (or plot) will show the colours as expected. This appears to be a bug of some sort in Matlab.

   If you want to see the colours in Matlab itself, try this:

    set(findobj('tag','m_grid_color'),'facecolor','none') 
   

14. Changes since last release

1. Many, many internal changes in the way coastlines are handled. Code functionality shifted, rearranged, etc. These changes should NOT be visible to the user, please let me know if they are!

2. m_scale, m_track, m_plotbndry, m_range_ring primitives

3. Some small bugs in the patch algorithm for coastlines corrected.

4. UTM projection

5. Extented m_ungrid usage to all available plot elements (grids, coastlines, etc.)